The energy functional to be minimized:
/n - 1 \
|----- |
----> | \ |
H(theta)= -J | ) cos(theta[i] - theta[i + 1])| -
| / |
|----- |
\i = 0 /
( 1 )
/ n \ / n \
|----- | |----- |
| \ 2 | | \ |
- A | ) cos (theta[i])| - h M | ) cos(theta[i])|
| / | | / |
|----- | |----- |
\i = 0 / \i = 0 /
where J is the interlayer coupling constant, being
negative for the case of antiferromagnetic coupling (J<0).
A is the anisotropy term, and M is the
individual layer magnetisation.
The model behind (1) is intended to describe the Fe/Cr(211) multilayer system grown on Mg(110) which develops a strong in-plane anisotropy within the plane of the layers in the Fe(011) direction. Since the Fe spins are tightly bound within the Fe layer, the magnetisation vector of layer may be modelled by a large (consequently classical) spin vector. The following physical parameters are used in the calculations (1):
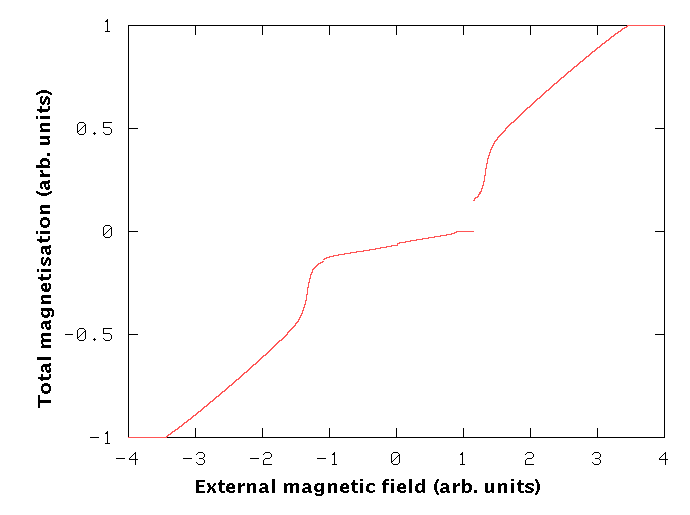
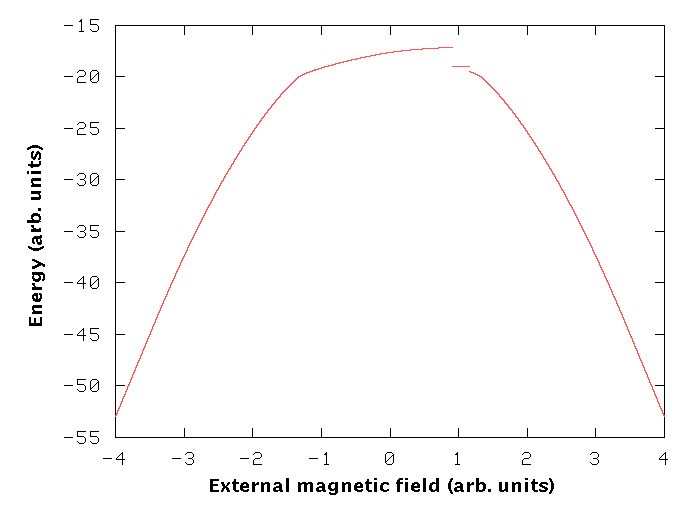
To gain a deeper insight into of the effects of the finite number of layers, first we calculated the above system without the anisotropy term (A=0). Click here for a detailed discussion. Below it is shown what happens if A=0. In the following 'mag(net)ic movies' increasing external fields are represented by a time evolution. Red arrows and the blue arrow on top represent the magnetisation vectors of the Fe layers and the applied external magnetic field, resp., the latter in units of J/4*M.


The 'jumps' in
the total magnetisation correspond to wild rearrangements of the layer
spin orientation as one can see in the following presentation - (may be sloooow). On the following
movie a faster version is displayed (it loops ... and loops again ...).
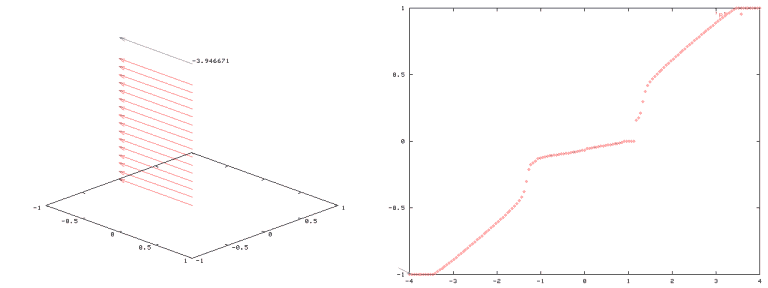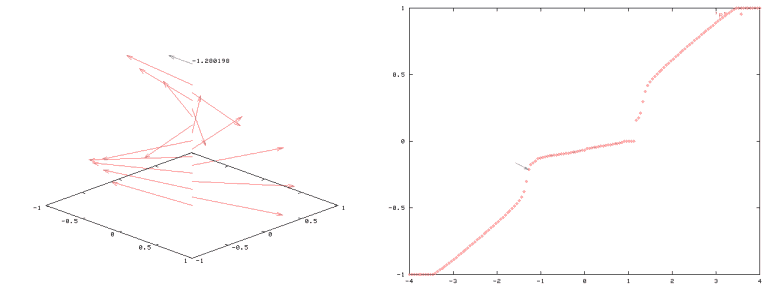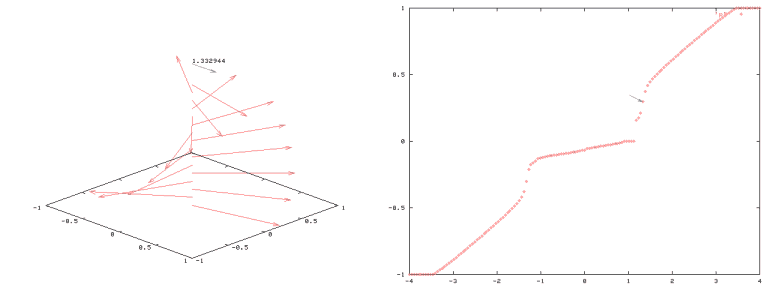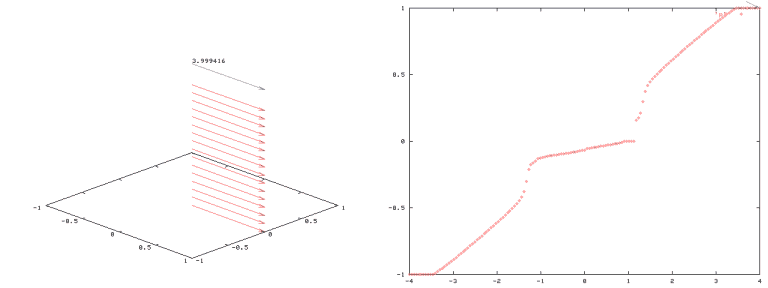
Of particular interest is the surface spin flop state in which the magnetisation jumps almost 180 deg from field-antiparallel to field-parallel orientation. Such jump occurs at about h=1. A 'zoomed' image of this region is displayed here. I hope you enjoyed it. I did, anyway.