400x400 no border

This demonstration is similar to the previous one. The only difference is, that now there is no border at the distribution. It is achieved by using a 500x500 grid, then cuting 50 pixels from each edge with pnmcut. Now also the random seed numbers are on-line together with the use source code thus one can repeat and check the results.

First again the primary distribution with a Gausian smooth of "smoothing width"=1.

void smooth(float *uncorr,float *corr,int id,float width)
{
#define GAUSS(X,Y,W) exp(-(X*X+Y*Y)/(2.0*W*W))

  /*  float uncorr[id*id],corr(id*id); */
  int i,j,id1,id2;
  int iw3,k,l;

  for(i=0;i<id*id;++i)
    corr[i]=MIN_LIM; /* Extremely low value = -inf */
  iw3=3*width;
  id1=iw3+1;
  id2=id-id1+1;
  for(i=id1-1;i<id2;++i){
    for(j=id1-1;j<id2;++j){
      corr[i*id+j]=0;
      for(k=-iw3;k<=iw3;++k){
        for(l=-iw3;l<=iw3;++l){
          if((k*k+l*l)<=iw3*iw3){
            corr[i*id+j]=corr[i*id+j]+GAUSS(k,l,width)*uncorr[(i+k)*id+(j+l)];
          }
        }
      }
    }
  }
}

The primary distribution (green=positive, red=negative) [seed=-1630451825]:

(Needs more than 256 color display to see in full depth)

The sign. distribution (eg. green=positive and zero, red=negative) of this distribution:

The subroutine which is responsible for this action:

void disp_gen(int id, float *corr, char *disp) 
{
  int i;

  for(i=0;i<(id*id);++i){
    disp[i]=(corr[i]>=0?1:0); /* instead of SIGN */
  }
}

From this primary distribution one can generate all the others. When the model system "opens" at saturation (the external magnetic field lowers) then one can get (seed=-528593744):

It is intresting to see the domain formation process itself:

At the Bulk Spin-flop (BSF) transition the secondary distribution is relevant. In our case it is a distribution of Gausian smothing of 5 pixels (seed=-1868308421.

The secondary distribution

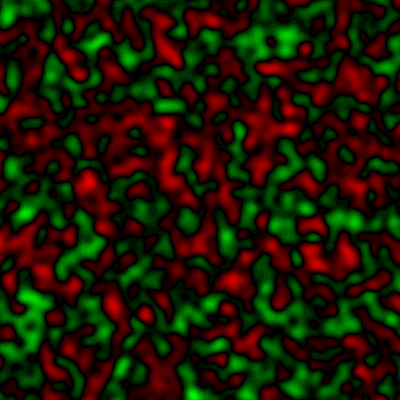
In the easy direction BSF transition the red-green will transform to blue-magenta (from left-right to up-down for example). The seed before the process: -1059265536.

The new state	The process

In the hard direction one will have four possibilities and the result is a small correlation lenght distribution screened by a long length one. (seed=-339322620).

The new state	The process