Paper published in Physical Review Letters 79, 3518 (1997)

We have observed a strong (2%) angular modulation of the total back-scattered conversion electron yield, measured as a function of the incidence angle of the 14.4 keV g-rays from a Moessbauer Co⁵⁷ source irradiating thin epitaxial Fe⁵⁷ film grown on MgO(001). The measured 2D pattern is the first hologram of the local surrounding of the absorbing nuclei obtained due to nuclear resonant scattering of g-rays. The real space hologram reconstruction shows distinct features corresponding to the nearest neighbor sites in bcca-Fe structure.

Holography with atomic resolution involving radiation from internal emitters was proposed by Szoeke [1] and it was applied in the last decade for direct imaging of surfaces, mainly using low-energy electrons [2-9]. Recently Tegze and Faigel [10] first discussed atomic resolution X-ray fluorescence holography (XFH) for bulk crystals. They also suggested to use for holography g-rays which are emitted in resonant recoilless processes from nuclei embedded in a crystal (Moessbauer effect) [10,11]. A photon emitted in such process may reach a far-field detector directly (holographic reference wave) or it may be additionally scattered from closely situated nuclei (object wave). The interference of the two waves gives a single hologram. The unique total holographic pattern is formed if all emitter neighborhoods are equivalent.

Nuclear resonant scattering is ideally suited for an inner source holography. For the most popular Moessbauer transition 14.4keV in Fe⁵⁷ the wavelength of 0.86A allows atomic resolution. On the other hand, for this wavelength the nucleus can be treated as a point scatterer. Consequently, the resonant nuclear scattering is more isotropic [12] than X-ray Rayleigh electron scattering used for XFH [13]. Finally, the coherent g scattering is sufficiently strong (s_coh=3x10^-4A² [12] ). We have calculated that for a model Fe⁵⁷ cluster holographic oscillation should be 3% of the reference wave, compared to 0.1-0.3% observed in X-ray holograms [10,14]. Note also that the hologram acquisition time scales with a square of the effect. The cross section value is however small enough to justify the neglecting of self-interference effects [15].

In spite of its promising perspectives, a straightforward realization of g-holography, as proposed by Tegze and Faigel [11], is experimentally difficult. A monocrystalline sample of Fe⁵⁷ (only 2.18% abundance) has to be made into a strong radioactive source by introducing Co⁵⁷. Because of the high value of the internal conversion coefficient for the 14.4keV transition (a=8.21) one needs a few tens mCi strong source to obtain a hologram in a reasonable time (months).

The additional difficulty in g-holography is due to a strong Bragg diffraction obvious for single crystalline samples. Bragg diffraction of g-rays, observed for the first time by Black and Moon [16], is presently in common use for nuclear resonant scattering of synchrotron radiation [17]. For internal sources coherent long range interference effects manifest themselves as Kossel lines [18], similar to those for X-rays. The Kossel line pattern begins to form if the number of scatterers contributing coherently to the pattern is of the order of 5x10⁴ [11]. However, because of the high spatial frequency one can try to filter it out numerically [10,11,14].

Moessbauer holography can in fact be done more efficiently by applying the optical reciprocity theorem as generalized for magneto-optical systems [18]. A classical version of this idea was recently applied to X-ray holography by Gog et al. [14], who developed XFH into multiple-energy X-ray holography (MEXH). In this method, which can be seen as a time reversal of XFH, the positions of the source and the detector are interchanged. The plane wave from a far field source reaches an atom in a sample (the microscopic detector of the hologram) directly or after being scattered on neighboring atoms. The measured quantity is the total fluorescence yield. Via the MEXH method X-ray holography may be done using strong synchrotron sources. Elimination of twin images becomes possible by applying a multi-energy hologram reconstruction algorithm, as successfully applied previously to electron holography [4,5,7-,9].

In a similar way but without the multiple-energy option we have performed "inverse" g-ray Moessbauer holography as shown in Fig.1(a). A photon from an external g-source can be absorbed in the recoilless resonant process by a nucleus in a crystal or it can be additionally resonantly scattered. The interference of these processes gives holographic oscillations of the total number of deexcitation events measured as a function of the g-ray incidence angle. Rayleigh electron scattering (as in XFX and MEXH) gives also a certain contribution to the hologram (about 20%, as estimated from the correspomding cross section values [12] ). The possible deexcitation products are reemitted g-rays and products of internal conversion: X-rays and electrons. In the case of Fe⁵⁷ the detection of electrons, 7.3 keV K- and 13.6 keV L-conversion electrons as well as 5.4 keV KLL and 6.2 keV KLM Auger electrons is the most efficient. The small electron escape depth (2000A for inelastically scattered electrons) compared to g and X-rays is compensated by the high value of the internal conversion coefficient and an easy detection over the full solid angle using a proportional flow detector.

The method requiring a single-crystal compound of iron containing only the Fe⁵⁷ isotope seems to be impractical. Thin epitaxial films which are relatively easy to prepare using molecular-beam epitaxy (MBE) make an exception. Moreover, Moessbauer measurements using conversion electrons are very efficient, permitting us to obtain a spectrum even for a single atomic layer of iron [19].

In our experiment we have used a 2000A Fe⁵⁷ film epitaxialy grown by MBE on a polished 10x10x1mm³ MgO(001) single crystal substrate held at 430K. LEED and XRD measurements proved that the film consisted of small (001)Fe⁵⁷ crystallites oriented with respect to MgO substrate in such way that Fe[100] direction was parallel to MgO[110] one. Similarly grown films of natural iron were investigated by us using in situ scanning tunneling microscopy. For 200A films we observed an island growth with the average diameter of 100A. This value coincides well with broadening of the LEED and XRD peaks observed for our holographic sample. Characterization of our sample, by the magneto-optic Kerr effect showed a narrow hysteresis loop of Kerr rotation with the coercive field of 20 Oe and the in-plane easy magnetization axis parallel to [100].

The system described above fulfills ideally the requirements of holographic experiment. Almost all absorbing nuclei have the same local surrounding, but the long range periodicity is disturbed by the island-like structure of the film. This attenuates long-range interference effects and reduces strong but unwanted phenomena such as X-Ray Bragg scattering or Kossel lines[19,20].

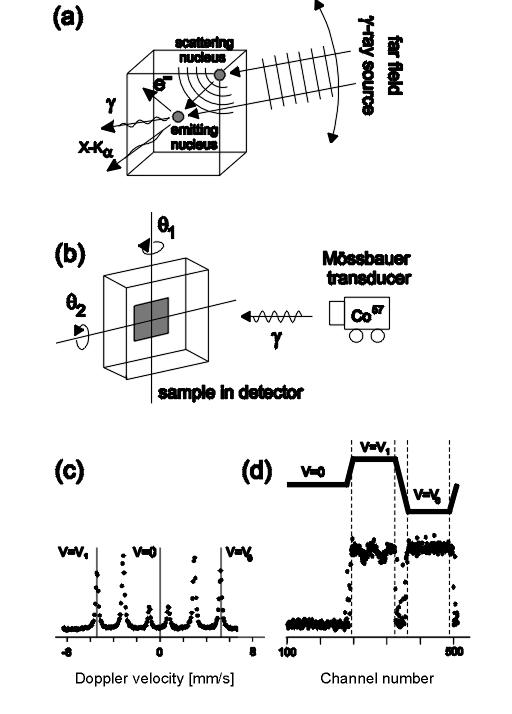
The sample was placed inside the conventional He/CH₄ filled proportional electron counter [21]. The sample, together with the detector, could be rotated about two perpendicular axes [100] and [010] (lying in the plane of the sample) by angles q₁ and q₂ respectively, as shown in Fig.1(b). This geometry of rotation was chosen because of the expected two-fold pattern symmetry - the measurement was performed in the remanent state, after saturating the film magnetization in the [100] easy direction.

A conventional 100 mCi Co⁵⁷(Rh) g-ray source of 8mm diameter was moved by a Moessbauer velocity transducer. The sample-detector distance was 15 cm. The transducer was driven in a three-constant-velocity mode. Two of the velocities corresponded to the outermost lines (circularly polarized ) of the previously measured Moessbauer spectrum (Fig. 2(c)). The third one (v=0), corresponding to an off-resonance condition, was used for data normalization. The acquisitions were made separately for each velocity using multiscaler time synchronized with the signal fed to the transducer (Fig.1(d)). The total number of counts in channels corresponding to a constant and well defined velocity, normalized to the total of non-resonant counts, was taken as the single pixel value of the pattern. Normalization was necessary to overcome time instabilities of the detection.

The original pattern was recorded on a dq₁ x dq₂ = 1.8x 1.8degxdeg angular mesh in the range from -43.2 to +43.2deg for both angles.

Fig. 2(a) shows 1D q₂-scans of the normalized electron yield obtained for a fixed value of the slow-scan angle q₁. The full pattern of raw (normalized) scans obtained in about 120 hours is presented in Fig. 2(b). The number of counts for this pattern is of the order of 5x10⁵ per pixel. As expected, holographic oscillations of about 2% are visible. A slow varying background was derived by Gaussian low-pass convolution as described by Harp et al. [22] and then substracted from the pattern. Additionally, a low-pass Gaussian filter was applied to the resulting pattern in order to eliminate noise. The processed hologram interpolated to a convinient k space mesh is presented in Fig 2(c). The hologram multiplied by the apodizing window function was then reconstructed to a real space using the Helmholz-Kirchoff formula [2]. Two-dimensional slices of the real space reconstruction obtained from the non-symmetrized hologram are shown in Fig.3. Slices in the (001) plane parallel and in the (010) plane perpendicular to the film surface, both at the distance of 1.43A from the emitter ( the interplanar spacing for bcc Fe) are presented in Figs.3(a,b), respectively. The positions of tha actual atomic crystal sites correspond to the centers of depicted ellipses. The theoretical resolution resulting from the accessible k range is reflected in the lengths of their axes. Roughly, the lateral resolution Dx=0.76A and vertical resolution Dz=3.12A were calculated according to Ref. [23]. The most intensive features of the reconstruction overlap with the nearest neighbors position in a-Fe. A small but visible asymmetry in both the measured pattern and in the holographic reconstruction is caused by strong polarization effects and/or interference between nuclear resonant and Rayleigh electronic scattering [12,16,17,24,25]. This is associated with the fact that nuclear transitions in Fe⁵⁷ are pure M1 and the system is uniformly magnetized. One has also to consider experimental errors in the sample orientation and the asymmetric response function of the detector. All geometrical uncertainties, including a finite size of the source and a coarse grid used for the acquisition of the hologram, are responsible for small shifts of the predominant features of the hologram reconstruction (positions of nuclei) from the true crystal positions. The holographic reconstruction does not go beyond the first coordination shell. This limitation is mainly caused by a rather poor statistic which in turn forced us to use the low pass filter, but also by a cancellation of real and twin images. The cancellation may be present in systems with high symmetry. It is caused by a different phase behavior of real and twin images as a function of the radiation energy used and as a function of the scatterer position relative to the hologram detector (see Refs. [11,13,26] ). The modest vertical resolution, (compare Fig 3(b)), additionally deteriorated by the overlapping of the real and twin images, could be improved by modifying the detector to have a higher acceptance angle for incident g-rays. For a full hemisphere the resolution could be better than 0.76A for both directions. Other visible features are artifacts due to the aliasing effects, arising in the transform, which are difficult to remove because of the low signal-to-noise ratio. Some of the above effects can be easily suppressed by a simple two fold-symetrization of the hologram.

To summarize, we have presented the first experimental demonstration of a new method for accomplishing atomic resolution holography based on resonant nuclear scattering of g-rays. To record the hologram we have used a conventional Moessbauer experimental setup. By tuning to a particular Moessbauer transition one is able to image individual crystal sites, as determined by a defined set of hyperfine interaction parameters. It should be possible to apply g-ray holography as a direct visualization tool for crystallographic and magnetic structures of epitaxial layers containing effectively just 100 atomic layer of Fe⁵⁷ isotope.

The authors are greatly indebted to Professor Marek Szymonski of the Institute of Physics, Jagiellonian University for inspiration. This work was supported by Polish Science Research Council, grants no. 2 P03B 080 10 and no. 2P03B 069 13.

[1] A. Szoeke, in Short Wavelength Coherent Radiation: Generation and Application, edited by D.T. Attwood and J. Bokor, AIP Conf. Proc. No. 147 (AIP, New York, 1986)

[2] J.J. Barton, Phys. Rev. Lett. 61, 1356 (1988)

[3] G. R. Harp, D. K. Saldin, and B. P. Tonner, Phys. Rev. Lett. 65, 1012 (1990)

[4] J. J. Barton, Phys. Rev. Lett. 67, 3106 (1991)

[5] S. Y. Tong, Hua Li, and H. Huang, Phys. Rev. Lett. 67, 3102 (1991)

[6] S. Thevuthasan, R. X. Ynzunza, E. D. Tober, C. S. Fadley, A. P. Kaduwela, and M. A. Van Hove, Phys. Rev. Lett. 70, 595 (1993)

[7] L. J. Terminello, J. J. Barton, and D. A. Lapiano-Smith, Phys. Rev. Lett. 70, 599 (1993)

[8] C. M. Wei, S.Y. Tong, H. Wedler, M. A. Mendez, and K. Heinz, Phys. Rev. Lett. 72, 2434 (1994)

[9] L. S. Caputi, O. Comite, A. Amoddeo, G. Chiarello, S. Scalese, E. Colavita, and L. Papagno. Phys. Rev. Lett 77, 1059 (1996)

[10] M. Tegze and G. Faigel, Nature 380, 49 (1996)

[11] M. Tegze and G. Faigel, Europhys. Lett. 16, 41 (1991)

[12] J. P. Hannon and G. T. Trammel, Phys. Rev. 169, 315 (1968); Phys. Rev. 186, 306 (1969)

[13] P. M. Len, S. Thevuthasan, C. S. Fadley, A. P. Kaduwela, and M. A. Van Hove, Phys. Rev. B50, 11275 (1994)

[14] T. Gog, P. M. Len, G. Materlik, D. Bahr, C. S. Fadley, and C. Sanchez-Hanke, Phys. Rev. Lett 76, 3132 (1996)

[15] S. Thevuthasan, G. S. German, A. P. Kaduwela, R. S. Saiki, Y.J. Kim, W. Niemczura, M. Burger, and C. S. Fadley, Phys. Rev. Lett. 67, 469 (1991)

[16] P. I. Black and P.B. Moon, Nature 188, 481 (1960)

[17] G. V. Smirnov, Hyp. Int. 97/98, 551 (1996); R. Rffer and A. I. Chumakov, 97/98, 589 (1996)

[18] J. P. Hannon, N. J. Carron, and G. T. Trammell, Phys. Rev B9, 2791 (1974); Phys. Rev. B9, 2811 (1974)

[19] J. Korecki and U. Gradmann, Phys. Rev. Lett. 55, 2491 (1985)

[20] T. Gog, D. Bahr, and G. Materlik, Phys. Rev. B51, 6761 (1995)

[21] K. R. Swanson and J. J. Spijkerman, J. Appl. Phys. 41, 3155 (1970)

[22] G. R. Harp, D. K. Saldin, X. Chen, Z.-L. Han, and B. P. Tonner, J. Electron Spectrosc. Relat. Phenom. 57, 331 (1991)

[23] J. J. Barton, J. Electron Spectrosc. Relat. Phenom. 51, 37 (1995)

[24] L. Y. Clark and C. D. Goodman, Phys. Rev. C6, 836 (1972)

[25] P. M. Len, T. Gog, D. Novikov, R. A. Eisenhower, G. Materlik, and C. S. Fadley, Phys. Rev. B56, 1229 (1997)

[26] P. M. Len, T. Gog, C. S. Fadley, and G. Materlik, Phys. Rev. B55, R3332 (1997)

Fig.1. The basic concept of "inverse" g-ray Moessbauer holography. (a) A photon from an external g-source irradiating an ordered sample at variable angle is directly adsorbed by nucleus or is additionally scattered by nearby nuclei. The hologram is formed due to interference of these processes. The deexcitating nucleus is a microscopic detector of the hologram. (b) Experimental setup. A conventional Moessbauer spectrometer is modified to enable the rotation of the detector (flow proportional electron counter). (c) Conversion electron Moessbauer spectrum of the holographic sample ( the velocities used for hologram acquisition are marked). (d) The drive signal fed to transducer moving in the three-constant-velocities mode and the corresponding content of multiscaler channels.

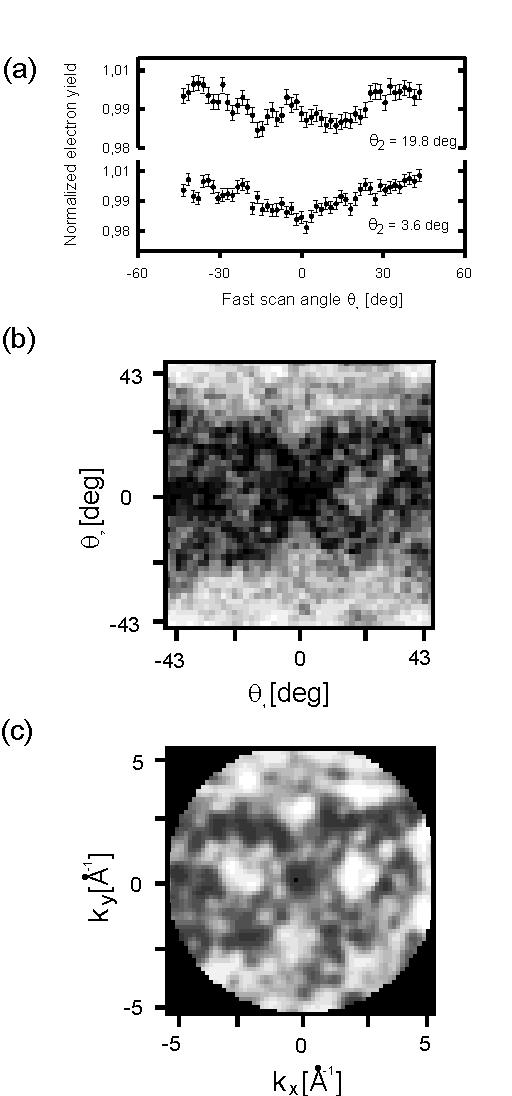
Fig.2 (a) q₂-scans of the normalized electron yield obtained for the fixed values of the slow-scan angle q₁. (b) The full pattern of the normalized scans. (c) The hologram in the k-space obtained from the pattern presented in (a) after the background removal and the low-pass filtering.The maximum osciallations are about 2%.

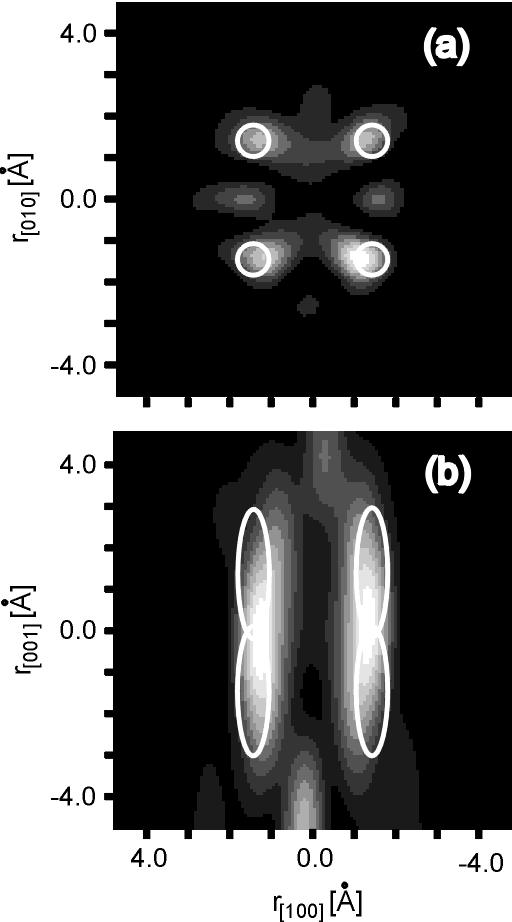
Fig.3. Holographic reconstruction of atomic poisition: (a) A (001) cut in a plane 1.43A from the emitter. (b) A (010) cut in a plane 1.43A from the emitter. The ellipses have dimensions equal to theoretical resolution in various directions and are centered on atomic sites.